이 문서는 baeldung의 문서를 번역하여 참조했습니다.
https://www.baeldung.com/java-graphs
먼저 그래프의 구성요소에 대해 알아보자.
그래프는 정점(Vertex)과 간선(Edge)으로 구성된다.
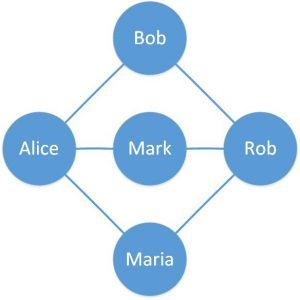
여기서 간선과 정점의 개수를 파악해보자. 정점은 5개, 간선은 6개로 구성되어있다.
그래프는 세 가지 종류로 구성된다. 크게 무방향 그래프, 방향 그래프, 가중치 그래프로 나뉜다.
무방향 그래프는 방향이 없는 간선이 두 정점을 연결하는 그래프이다.

방향 그래프는 방향이 있는 간선이 두 정점을 연결하는 그래프이다.
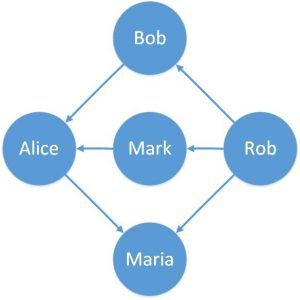
가중치 그래프는 각 간선마다 가중치가 설정되어 있는 그래프이다.

그래프는 비선형 자료구조이다. 연결리스트, 스택, 큐와 같은 선형 자료구조와는 다른 방법으로 표현 방법을 구성해야 한다. 이 과정에서 인접 리스트 그리고 인접 행렬이라는 두 가지 방법이 사용된다. 그리고 탐색하는 방법은 선형구조처럼 단순하지 않다. 우선 가장 많이 쓰이는 알고리즘은 너비 우선 탐색(BFS)과 깊이 우선 탐색(DFS)이다. 알고리즘의 분류에서 BFS나
두번째로, 표현 방법인 인접 리스트와 인접 행렬에 대해 알아보자.
인접 리스트는 하나의 정점에 대해서 한 개의 간선으로 인접한 정점을 리스트 형태로 표현한 것을 의미한다. 아래는 위의 그래프를 인접 리스트 형태로 표현한 구조이다.

다음으로 인접 행렬에 대해서 알아보자. 선형대수학에서 사용하는 행렬, 그 중에서도 2차원 배열을 이용한 그래프 표현 방법이다.
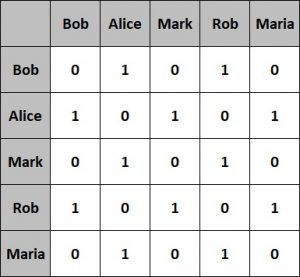
0과 1이 의미하는 것은 두 정점이 간선으로 직접 연결되어 있다는 것을 의미한다.
우선 대각성분(행과 열이 같은 성분, 예를 들면 1행 1열, 2행 2열....)은 모두 0이다. 당연하지만 자신과 자신은 간선으로 연결되어 있지 않기 때문이다. 여기서 몇 가지 예를 들면 Bob과 Alice는 직접 연결되어 있으므로 1이며, Bob과 Mark는 직접 연결되어 있지 않으므로 0이다.
세번째로, DFS와 BFS에 대해 알아보자.
이 두 알고리즘은 탐색 알고리즘을 그래프에 적용한 내용이다.
BFS는 너비 우선 탐색을 의미한다.
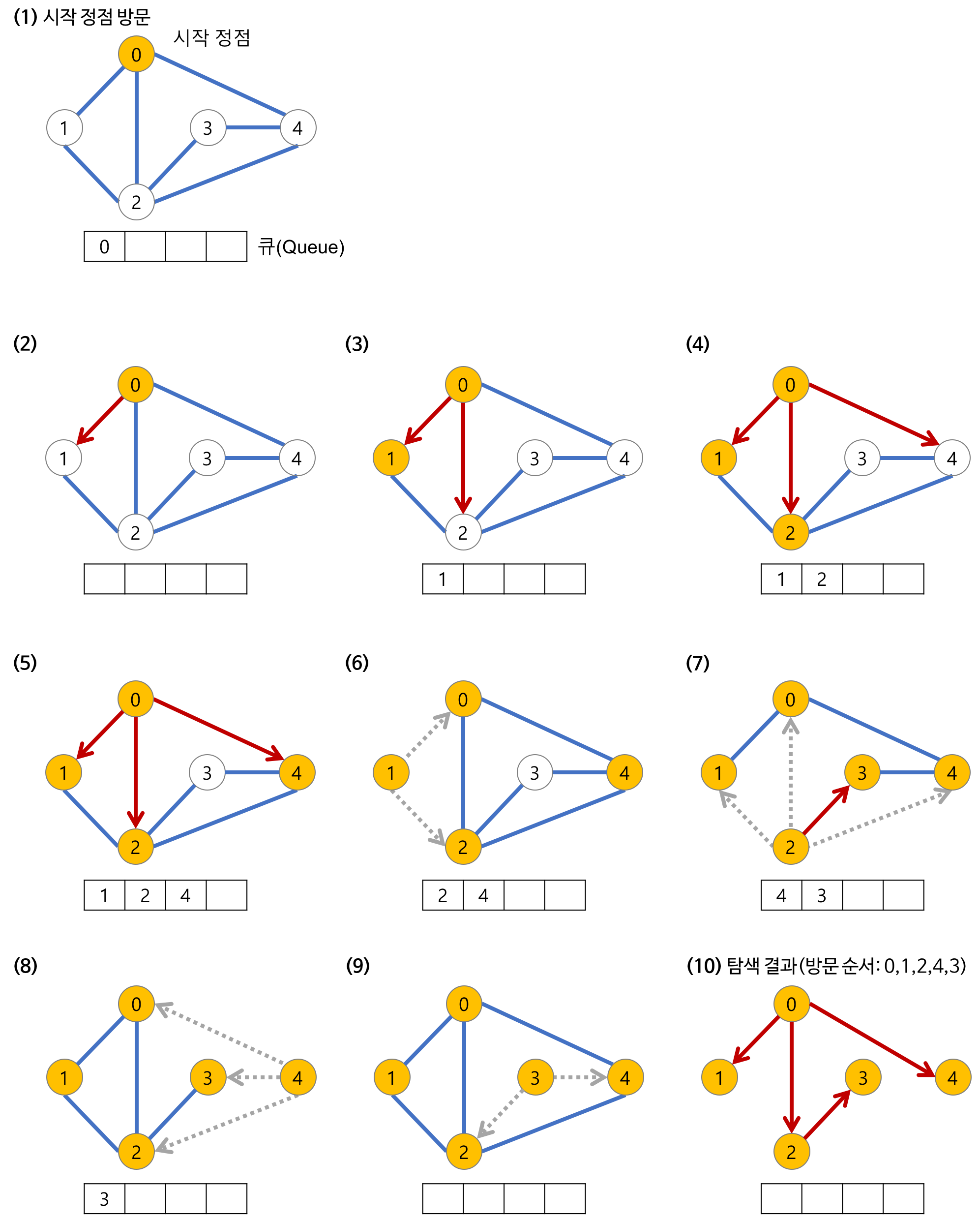
DFS는 깊이 우선 탐색을 의미한다.
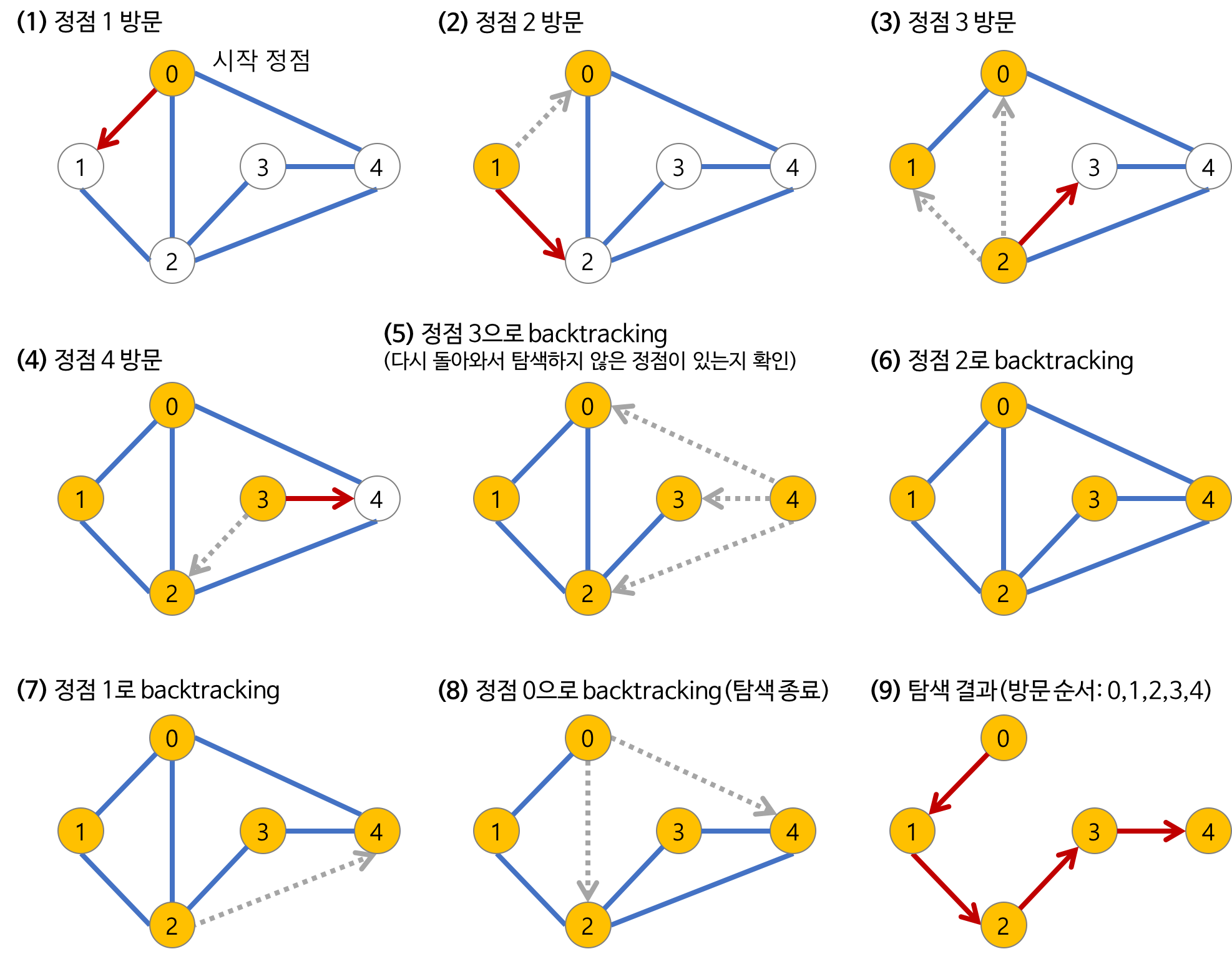
마지막으로 자바로 이를 구현해보자.
package 원석.ch12;
import java.util.*;
class Graph {
private Map<String, List<String>> adjacencyList;
public Graph() {
this.adjacencyList = new HashMap<>();
}
public void addNode(String node) {
adjacencyList.put(node, new ArrayList<>());
}
public void addEdge(String source, String destination) {
if (!adjacencyList.containsKey(source)) {
addNode(source);
}
if (!adjacencyList.containsKey(destination)) {
addNode(destination);
}
adjacencyList.get(source).add(destination);
}
public void removeNode(String node) {
adjacencyList.remove(node);
// Remove edges containing the removed node
for (List<String> neighbors : adjacencyList.values()) {
neighbors.removeIf(neighbor -> neighbor.equals(node));
}
}
public void removeEdge(String source, String destination) {
List<String> neighbors = adjacencyList.get(source);
if (neighbors != null) {
neighbors.remove(destination);
}
}
public void displayAdjacencyList() {
for (Map.Entry<String, List<String>> entry : adjacencyList.entrySet()) {
String node = entry.getKey();
List<String> neighbors = entry.getValue();
System.out.print("Node " + node + " is connected to: ");
for (String neighbor : neighbors) {
System.out.print(neighbor + " ");
}
System.out.println();
}
}
public void dfs(String startNode) {
Set<String> visited = new HashSet<>();
Stack<String> stack = new Stack<>();
stack.push(startNode);
while (!stack.isEmpty()) {
String currentNode = stack.pop();
if (!visited.contains(currentNode)) {
System.out.print(currentNode + " ");
visited.add(currentNode);
for (String neighbor : adjacencyList.get(currentNode)) {
stack.push(neighbor);
}
}
}
}
public void bfs(String startNode) {
Set<String> visited = new HashSet<>();
Queue<String> queue = new LinkedList<>();
queue.add(startNode);
while (!queue.isEmpty()) {
String currentNode = queue.poll();
if (!visited.contains(currentNode)) {
System.out.print(currentNode + " ");
visited.add(currentNode);
for (String neighbor : adjacencyList.get(currentNode)) {
if (!visited.contains(neighbor)) {
queue.add(neighbor);
}
}
}
}
}
}
public class Main {
public static void main(String[] args) {
Graph graph = new Graph();
// 노드와 간선 추가
graph.addNode("Bob");
graph.addNode("Alice");
graph.addNode("Mark");
graph.addNode("Rob");
graph.addNode("Maria");
graph.addEdge("Bob", "Alice");
graph.addEdge("Rob", "Bob");
graph.addEdge("Mark", "Alice");
graph.addEdge("Rob", "Mark");
graph.addEdge("Alice", "Maria");
graph.addEdge("Rob", "Maria");
// 인접 리스트 출력
System.out.println("Graph after initial additions:");
graph.displayAdjacencyList();
// DFS 수행 및 출력
System.out.print("\nDFS: ");
graph.dfs("Bob");
// BFS 수행 및 출력
System.out.print("\nBFS: ");
graph.bfs("Bob");
// 노드와 간선 삭제
graph.removeNode("Mark");
graph.removeEdge("Bob", "Rob");
// 삭제 후 인접 리스트 출력
System.out.println("\nGraph after removals:");
graph.displayAdjacencyList();
}
}
인접 리스트 출력 결과는 아래와 같다.
Graph after initial additions:
Node Bob is connected to: Alice
Node Rob is connected to: Bob Mark Maria
Node Alice is connected to: Maria
Node Mark is connected to: Alice
Node Maria is connected to:
BFS, DFS의 과정과 출력 결과를 살펴보자.
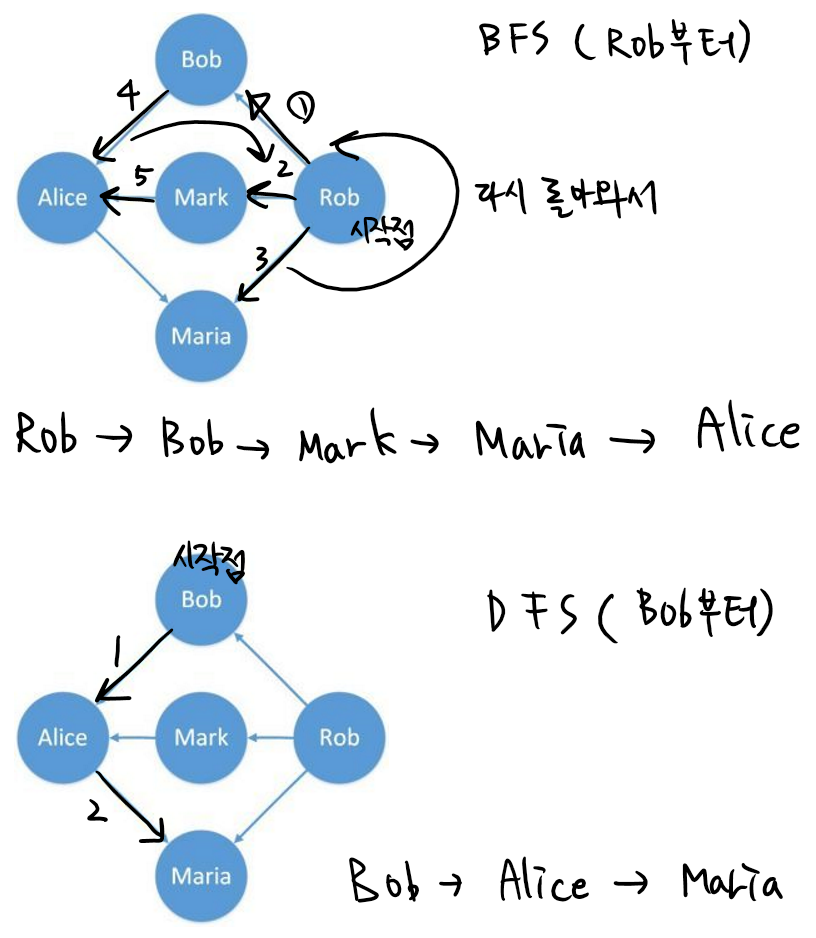
DFS: Bob Alice Maria
BFS: Rob Bob Mark Maria Alice
다음으로 여기서 Mark를 제거하고 그 코드에 대한 출력 결과를 보자.

Graph after removals:
Node Bob is connected to: Alice
Node Rob is connected to: Bob Maria
Node Alice is connected to: Maria
Node Maria is connected to:'Portpolio > java_algo_interview' 카테고리의 다른 글
| 자바 알고리즘 인터뷰 14. 트리 (0) | 2024.02.16 |
|---|---|
| 자바 알고리즘 인터뷰 13. 최단 경로 문제 (0) | 2024.02.16 |
| 자바 알고리즘 인터뷰 11. 해시 테이블 (0) | 2024.02.16 |
| 자바 알고리즘 인터뷰 10. 데크, 우선순위 큐 (0) | 2024.02.16 |
| 자바 알고리즘 인터뷰 09. 스택, 큐 (0) | 2023.12.31 |

댓글